Analytische Lösung von Differentialgleichungen ist nicht immer möglich

>

Geschwindigkeit: Änderung des Wegs über die Zeit: s´ = v

Beschleunigung: Änderung der Geschwindigkeit über die Zeit : v´ = a

Zusammenhang zwischen Weg, Geschwindigkeit und Beschleunigung:

s´´ =  v´ = a

>

restart;

>	a:=(t) ->8-16*t+3*Pi*cos(3*Pi*t);

>	plot(a(t),t=0..1);                       #Beschleunigung

>	dsolve({diff(v(t),t$1)=a(t)},v(t));

>	dsolve({diff(s(t),t$2)=a(t)},s(t));

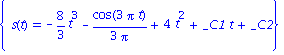
Bestimmung der Konstanten C1 und C2 durch gegebende Randbedingungen:

1.Fall: s(0)=0, v(0)=0;

Für s(0)=0:

0=4*0+8/3*0-cos(3*Pi*0)/(3*Pi)+C1*0+C2

C2=1/(3*Pi)

Für v(0)=0

0=8*0-8*0+sin(3*Pi*0)+C1

C1=0

>	dsolve({diff(s1(t),t$2)=a(t),D(s1)(0)=0,s1(0)=0},s1(t));

>	s1(t):=rhs(%):

>

s1(t);

>	plot(s1(t),t=0..1);                      #zurückgelegter Weg

2.Fall: v(0)=0, v(1)=1;

Für v(0)=0:
0=8*0-8*0+sin(3*Pi*0)+C1

C1=0

Für v(1)=1:

1=8*1-8*1+1*sin(3*Pi*1)+C1

C1=1

>	dsolve({diff(s2(t),t$2)=a(t),D(s2)(0)=0,D(s2)(1)=1},s2(t));

Diese Randbedingungen führen zu keiner Lösung

3.Fall: v(0)=0, v(1)=0:

Für v(0)=0:

0=8*0-8*0+sin(3*Pi*0)+C1

C1=0

Für v(1)=0:

0=8*1-8*1+sin(3*Pi*1)+C1

C1=0

C2 nicht definiert, d.h. unendliche viele Lösungen (abhängig von C2)

>

>	dsolve({diff(s3(t),t$2)=a(t),D(s3)(0)=0,D(s3)(1)=0},s3(t));

>	s3(t) := rhs(%):

>	with(plots):

Warning, the name changecoords has been redefined

>	animate( plot, [s3(t),t=0..1],_C2=0..7);

>

Bedingungen für:

- eine bestimmte Lösung

- keine Lösung

-unendlich viele Lösungen

- eine Lösung:

  - 2 Randbedingungen , wobei zumindest eine eine Funktion von s darstellen muss

- unendlich viele Lösungen:

  - 2 Randbedingungen der Geschwindigkeit

  - Resultat für C1 muss bei beiden Randbedingungen gleich sein

     Beispiel:

    v(t1)=v1 ... Geschwindigkeit zum Zeitpunkt t1

    v(t2)=v2 ... Geschwindigkeit zum Zeitpunkt t2

    => v1 - v2 = (8t1-8t1^2+sin(3*Pi*t1) - (8t2-8t2^2+sin(3*Pi*t2)

  als Integral ausgedrückt:

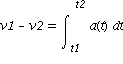
- keine Lösung:

  - 2 Randbedingungen der Geschwindigkeit

  - Resultat für C1 muss bei den beiden Randbedingungen unterschiedlich sein